(This article was republished on steemit.com on 2016-07-12)
When bitcoin launched, a lot of people thought they finally had decentralised digital cash. We saw people using bitcoins for ideological reasons, but also for the presumed anonymous properties. You didn’t need to provide any identity information to create a wallet or send a transaction. Anonymous magic internet money. Cool, right?
Over the years, it became more clear that bitcoin isn’t anonymous at all. All transactions can be traced on the blockchain. If you transact with a stranger at a bitcoin meetup, he could start guessing your total bitcoin balance in your wallet. When you interact with regulated bitcoin businesses, you are required to provide ID information. And you can be sure that this company will couple your customer data to your blockchain fingerprint. This data can be handed over to law enforcement upon request, and be used to analyse the blockchain and associate more activity with you, or reveal connections with certain people, markets or online services.
A lot of bitcoin tracking companies started to deanonymize users by using this data and are actively trying to map the whole bitcoin blockchain.
So how can we avoid this bitcoin tracing?
Some people started to offer mixing services. These are centralised platforms where you send your coins to and you (hopefully) get coins back which aren’t related to your coins. The problem with this is that these platforms can be honeypots operated by law enforcement, or can just go offline and run with your money.
Another option is a form of coinjoin/joinmarket. This is a system where people let other people know they want to mix their coins. People eventually sign one big transaction with all the inputs of the people who wanted to mix at that certain point in time and get outputs from that transaction to a new address.
This somewhat breaks the link, but there is still a degree of traceability: once you get coins back in different outputs and you start transacting again, these outputs will probably be joined again and it’s possible some of the outputs can be linked to the inputs.
A sybil attack is also possible: when you mix with coinjoin, you assume these people are random, but these people could in fact all be law enforcement just waiting for the mixing transactions to happen. If you only “mix” with one party, that party knows your inputs and outputs, while you assume that you now own anonymous bitcoins. This is a very dangerous situation!
But the biggest issue isn’t even the centralized mixers running with your money, honeypots, or traceable coinjoins. It’s something that is -in my opinion- a very underestimated issue:
Enter fungibility.
Fungibility is a property of money that makes every unit if this money interchangeable: you can pay someone with a paper note and the receiver won’t care where it came from. As long as this note isn’t counterfeited, he will accept it and exchange goods or services for that paper note. This is how physical cash works.
But how do we enforce fungibility on a transparent blockchain where every transaction is visible?
All forms of mixing on transparent chains are active forms of mixing: if you want to mix coins, you need to find other people who want to mix as well. This makes the system vulnerable to sybil attacks/honeypots and, more importantly, people can see on the blockchain you tried to mix your coins. This act in itself could already be considered a crime: you are actively money laundering your coins.
Even if using a mixing service isn’t viewed as a crime, there are still a lot of fungibility risks associated with mixing. First and foremost, there is the possibility of blacklisting coins.
Even if you succeed in anonymizing your coins, there is still a trail. It’s pretty easy to know by analysing the blockchain that certain coins were sent to a darknet market for example. So if you try to mix your coins, you do that with coins from an unknown source (that’s the whole point, remember?).
Suppose that after mixing, you get coins back which were used in a drug transaction. Suppose the DEA busts a house of a drug dealer and follows the trail of the bitcoins that guy earned. The DEA may eventually find your wallet as the destination of the drug money. If you then spend these coins at a website that uses a payment processor, your customer data is connected with this drug money and you may get a knock on your door by law enforcement. If you try to sell these coins at an exchange, it’s possible your account will be blocked and your coins will be confiscated and sent to the government wallet. Certainly in the USA this is a risk because Civil Asset Forfeiture laws are broadly applied.
Another problem is mining censorship: miners confirm transactions. Up until now they seem to confirm any valid transaction. But what if law enforcement goes to the biggest miners in the world (representing at least 51% of the hashpower) and tells them that if they continue to confirm easily identifiable mixing transactions, they will be accused of money laundering. What if they aren’t even allowed to build new blocks on blocks containing such illegal transactions? It’s all possible in theory. Regulatory compliance by miners is -in my opinion- just a matter of time.
This is the fungibility problem that a transparent blockchain faces. Note that 99% of all cryptocoins are using a transparent blockchain, even the (in-)famous cryptocoin DASH, which just offers a form of CoinJoin that is built in the GUI wallet and mixes the coins on centralised “masternode servers” that can log every input and output.
Enter Monero.
What makes Monero different from all other cryptocurrencies? Well, unlike Bitcoin, it uses a passive form of mixing.
How does this “passive mixing” work?
Monero uses ring signatures to obfuscate transactions. When you create a transaction, your Monero client randomly selects some transactions from the monero blockchain and signs a “ring signature”. Along with this ring signature, some kind of “fingerprint” is published, called the key image. This results in a transaction where an observer can’t know who is the real signer, but has cryptographic proof that it’s a valid transaction and no double spend happened.
Because your client picked the other transaction outputs randomly, those outputs are obfuscated even more. And this happens without them signing anything. Their coins can even be stored on a paper wallet and still be included in your transaction! So when sending a transaction, you not only immediately have plausible deniability about your own transaction history, but also obfuscate the blockchain even more. You generate positive externalities when you transact. The more people are using monero, the better its privacy will become.
In Monero, ring signatures are combined with stealth addresses to also make it impossible to identify the receiver of the coins. A transaction is sent to a “one time address”. The receiver needs to constantly scan the blockchain with his private viewkey to know which transactions are meant for him. With his private spend key he can then create a ring signature and spend his coins. Soon Confidential Transactions will be added to Monero with the goal of also making the transaction amount invisible. This will also solve some small issues with Monero privacy that now still exist.
But what has this fancy mixing system to do with fungibility? It’s still possible to track coins and see that certain coins are mixed, right?
Well, no: the use of ring signatures is enforced by the Monero protocol. Unmixed transactions aren’t allowed on the Monero blockchain. This results in every transaction being in a ring signature and obfuscating the chain even more. This guarantees fungibility on 2 levels: it’s impossible to track coins due to the default mixing and nobody can prove that you initiated the mixing thanks to the plausible deniability features of ring signatures.
The only exception to this are the newly minted coins: these coins don’t have inputs, so they can’t be signed with a ring signature. But this is actually an advantage, as it makes it possible to verify that the amount of newly minted coins is according the the emission scheme. However, other transactions can include these minting transactions in a ring signature. So when that happened at least once, the miner has plausible deniability on whether he spent his freshly minted coins or not.
This means that accepting or spending Monero doesn’t have any risks of being tracked, blacklisted or censored. You simply don’t know what is happening but you can verify that no double spends are happening and that the supply scheme is honoured. Some issues still exist, but these are minor and are actively being researched by the Monero Research Lab. See their research papers for more info. Monero is an (almost) perfect form of digital cash.
Note that Monero will only give you the full benefits of its technology as long as you stay inside the system. Once you start using Monero as some kind of mixer by buying XMR with BTC and spending your XMR immediately after that, some timing analysis can happen based on the bitcoin and monero blockchain. You shouldn’t enter and exit the Monero system every time you want to transact anonymously. This would diminish the privacy and fungibility aspects of your transaction. In stead, you should just use the funds you already have stored in the network. Monero as a sidechain to Bitcoin is therefore not a good idea. People who actually store a part of their wealth in Monero, will benefit from the obfuscation created by other people transacting. Monero is therefore only useful as a separate fungible network.
 So what’s all that buzz around ZCash?
So what’s all that buzz around ZCash?
Isn’t that coin claiming to be completely anonymous and better than every other anonymous cryptocurrency out there?
ZCash is a cryptocurrency project that originated from the Zerocoin/Zerocash idea, proposed back in 2013. Almost every “old time” bitcoiner knows about it. It was proposed to be integrated in the bitcoin codebase so that you would have the option to send a zerocoin-transaction using the bitcoin blockchain. You would need to “pour” your bitcoins in the Zerocoin mixer and from that point onwards, you could transact anonymously using the Zerocoin-protocol. When it became clear that Zerocoin wouldn’t be implemented in the bitcoin codebase any time soon, they worked for a while on implementing it as a sidechain.
But at some point the Zerocoin-team pivoted and decided to launch the altcoin ZCash. There is nothing wrong with trying to launch an altcoin, but, in my opinion, an altcoin can only survive long term if it actually offers something that is unique and probably can’t be adopted by bitcoin. The fact that it’s possible to add ZCash as a sidechain to bitcoin, should already raise some red flags.
The ZCash team decided to launch ZCash as an altcoin so they were able to fund the development: ZCash has a US-based company behind it and will tax 20% of the mining revenue during the first 4 years to pay off private investors. If ZCash were to succeed, the private investors will benefit greatly from the launch of this cryptocurrency. Although I don’t like ICO’s, a public coinsale (a form of crowdfunding) would have been a more fair and open way to fund development than seeking money from private investors.
This is in great contrast with the launch of Bitcoin and Monero, which were fairly launched, without “premine”, “mining tax” or some kind of company behind it. In my opinion, a successful large cryptocoin will probably be grass-roots, but it’s possible I’m mistaken here. Maybe some people actually prefer a corporate coin like ZCash. Time will tell.
But let’s dive into the tech a bit to compare its features with Bitcoin and Monero. The first thing that strikes me is the fact that ZCash allows transparent transactions: mined coins are bitcoin-like transparent “base coins”. When you want to spend them, you have the option to do an anonymous “pour” to enter them into the ZCash mixer. It’s basically the same idea as using Zerocoin as a sidechain.
This ZCash mixer functions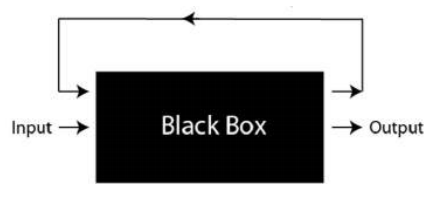 as a “black box”: you can see what is entering and what is exiting, but you can’t see what is happening inside the ZCash-mixer. This fact alone doesn’t magically make ZCash fungible: transparent transactions are still possible, so the mixing isn’t default.
as a “black box”: you can see what is entering and what is exiting, but you can’t see what is happening inside the ZCash-mixer. This fact alone doesn’t magically make ZCash fungible: transparent transactions are still possible, so the mixing isn’t default.
It’s also an active form of mixing, not a passive form like on the Monero network. Because you need more than 8GB of RAM to do an anonymous ZCash transaction, it’s very likely that the mixing won’t be enforced any time soon and, what’s even more concerning, the large majority of transactions will probably just be transparent bitcoin-like transactions. Another concern is “timing analysis”: if the ZCash mixer isn’t used much, you can try to connect coins entering the mixer with coins exiting the mixer. Certainly for larger transactions this is a real possibility.
The fact that transparent transactions are still possible, also makes your OpSec dependant on others: even if you try to anonymize your coins as much as possible, you can still be deanonymized if the people you transact with aren’t using the same standards. It’s even possible you’ll be forced to use transparent transactions if you want to use some kind of (regulated) service. This will result in the same issues as described on a transparent blockchain. Identities will be attached to addresses and this can eventually lead to blacklisting or even miner censorship. The fact that mixing isn’t enforced on ZCash is bad for fungibility and anonymity.
Another problem with ZCash is the fact that it’s brand new cryptography. Nobody can really guarantee that there aren’t some bugs in the system that will make it possible to deanonymize transactions or create coins out of thin air. What’s more, if coins are being created, it will not even be detectable because, unlike Monero, you can’t verify the total amount of coins in the ZCash blockchain. During the alpha test phase, they already found such a bug. Nobody can guarantee that similar bugs won’t exist when ZCash launches. It doesn’t seem a great idea to base a monetary system on brand new crypto. Accidents can happen, and when they happen, the value will plummet.
Related to this issue of brand new cryptography is that some features like multisig are not that hard to implement on Monero, while for ZCash this will require a lot of research. Meanwhile, ZCash will probably use the bitcoin-styled multisig on the transparent part of the network.
The ZCash extended paper also mentions a theoretical “poison pill attack” (section 6.4). This attack makes it possible to target a single user with the goal of deanonymizing him. It seems this attack is easier to perform when the targeted user uses an anonymous network like Tor. Monero, in contrast, is integrating with I2P.
 Another problem ZCash faces is the “trusted setup”, the so called cryptographic “toxic waste” problem. This is some data that is needed when the initial parameters of ZCash are created, but needs to be deleted afterwards. If somehow someone gains access to this “toxic waste”, this entity can create coins out of thin air without anyone noticing. This is a serious problem because this makes a malicious backdoor in ZCash a real possibility.
Another problem ZCash faces is the “trusted setup”, the so called cryptographic “toxic waste” problem. This is some data that is needed when the initial parameters of ZCash are created, but needs to be deleted afterwards. If somehow someone gains access to this “toxic waste”, this entity can create coins out of thin air without anyone noticing. This is a serious problem because this makes a malicious backdoor in ZCash a real possibility.
The fact that ZCash is a US-based company, doesn’t really help with building confidence in this cryptocurrency. It’s not unthinkable some agency will require the ZCash team to make a copy of this “toxic waste” and hand it over to them. Just google what the US government did to the owners of e-gold, Liberty Reserve and the Liberty Dollar, and you’ll understand what kind of pressure they can exert on the owners of the ZCash company. If coins can be created at will, the inflation will diminish the value of the coin.
There is a clear trade-off between using Monero or Zcash: Monero is a usable and default fungible cryptocurrency based on solid cryptography without “trusted setup” by a company. The whole Monero blockchain becomes more and more obfuscated over time when people are transacting, which mitigates the “imperfect” anonymity. Meanwhile, the anonymity of Monero is also being improved on a technical level by the Monero Research Lab.
ZCash on the other hand has a different approach. They offer a completely anonymous mixer, but not by default, resulting in fungibility and anonymity problems. It has some serious issues related to the “toxic waste” during the “trusted setup” and has a lot of additional risks due to the brand new cryptography that is being applied.
Is it an interesting research project? For sure. Should it be applied in a cryptocurrency? No.
Sidenote: it’s perfectly possible to add a ZCash mixer to the Monero blockchain. In that case the “base coins” are the normal Monero-tokens that already are in circulation and people can choose to send their coins to a ZCash sidechain. The Monero network will need to check if the total number of XMR that goes into the sidechain is always larger than the total number of XMR that is exiting the sidechain.
Even if a hacker finds an exploit to create XMR out of thin air inside the ZCash mixer, he will only be able to drain the sidechain, not the mainchain. Use of the ZCash sidechain is then at your own risk. No additional Monero can be created on the mainchain, which is still perfectly fungible.
EDIT: Zooko reached out to me to point out he didn’t start the zerocoin/zerocash project. He became involved at a later point in time. Article changed accordingly.
EDIT2: Zooko asked me to be less speculative about the motives surrounding the launch. I linked to the article he provided.


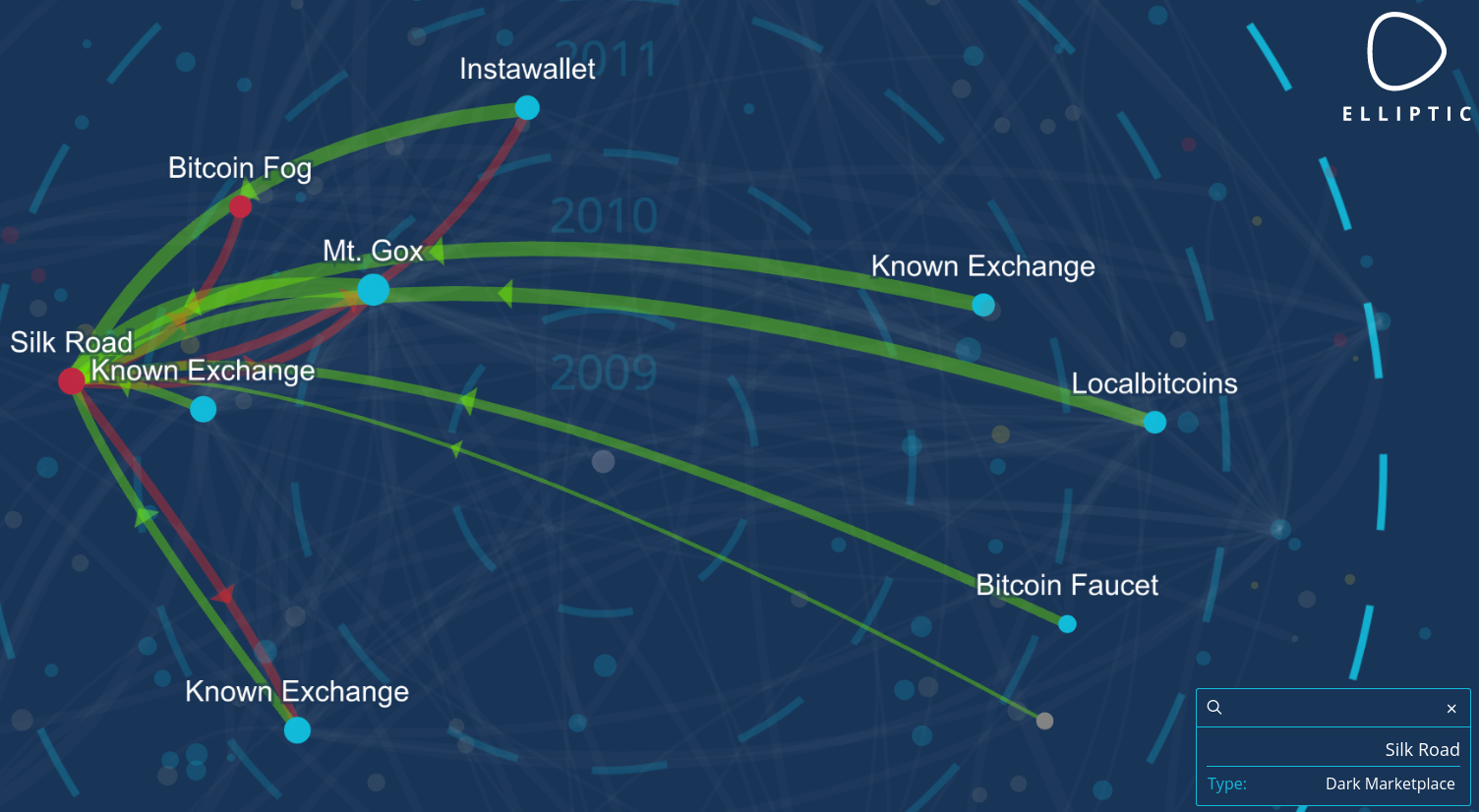


 A lot of bitcoins are lost because people are hacked. When a hacker gets access to you private keys, he can steal your money. Some people don’t want to take the risk to store their crypto themselves, so they leave it on the exchange. But that is also a big risk (do I need to remind you about Mt. Gox?)
A lot of bitcoins are lost because people are hacked. When a hacker gets access to you private keys, he can steal your money. Some people don’t want to take the risk to store their crypto themselves, so they leave it on the exchange. But that is also a big risk (do I need to remind you about Mt. Gox?)